近日，我校李劍教授團隊的研究成果“A decoupled, linear, unconditionally stable, and fully discrete finite element scheme for two-phase ferrofluid flows with different densities and viscosities”發(fā)表于計算物理領域國際頂級期刊 Journal of Computational Physics。我校博士生陳曉勇為第一作者，該研究工作與美國密蘇里科技大學何曉明教授共同完成，李劍教授與陜西師范大學李瑞副教授為共同通訊作者。陜西科技大學為論文的第一通訊單位。

鐵磁流體作為一種兼具液體流動性與固態(tài)磁響應特性的功能材料，可通過磁場實現(xiàn)精確操控。其獨特的磁-流耦合效應使其在微流控、生物醫(yī)學、航空、能源及工業(yè)應用等領域潛力巨大。鐵磁流體應用多涉及兩相流系統(tǒng)，其中一相具有磁性，另一相則無。2016年，R.H. Nochetto 等人在合理假設下，針對相同密度的兩相鐵磁流體流動問題，首次建立了相同密度模型并提出全耦合數(shù)值格式求解。截至當前，國際上在該模型基礎上提出了解耦、線性且無條件能量穩(wěn)定的一階或二階時間收斂數(shù)值格式，數(shù)學領域共有5篇論文發(fā)表。

然而，針對密度差顯著的兩相鐵磁流體系統(tǒng)，由于其復雜的多物理場強耦合特性（涉及流體動力學相分離與磁效應）及界面動力學行為，現(xiàn)有程序與軟件數(shù)值模擬均已失效。圍繞上述難點問題，本研究團隊聚焦于大密度差兩相鐵磁流體流動問題，建立不同密度和黏度的兩相鐵磁流體動力學模型。重構磁勢方程、引入人工可壓縮方法、采用隱式-顯式格式處理非線性項，提出了一種大密度差兩相鐵磁流體流動問題線性化解耦有限元方法。該格式無需對壓力場施加人為邊界條件，嚴格證明了它在每個時間步都是無條件穩(wěn)定和唯一可解的。在現(xiàn)有數(shù)值模擬和軟件失效的情況下，重新研制程序給出了相應的數(shù)值模擬。

據(jù)悉，Journal of Computational Physics (JCP) 是計算流體力學 (CFD) 和計算數(shù)學領域公認的頂級期刊。CFD 領域大多數(shù)具有原創(chuàng)性和實質改進意義的數(shù)值離散方法，其奠基性工作均發(fā)表在 JCP 上。

圖1 鐵磁流體Rosensweig不穩(wěn)定性圖(https://www.livescience.com/61426-ferrofluid-gif.html)

圖2 六個不同時刻下，非均勻磁場模擬的Rosensweig不穩(wěn)定性結果

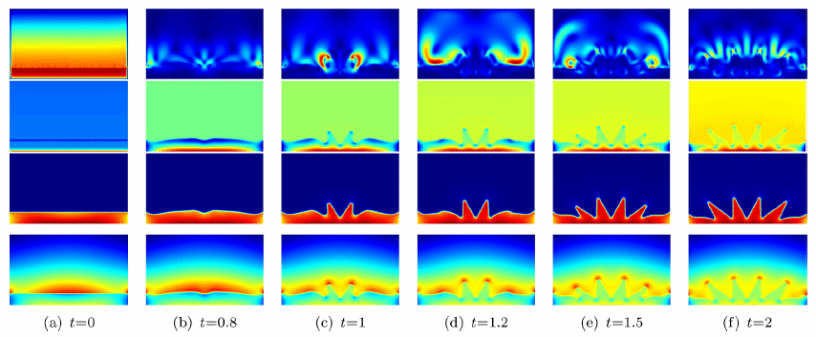
圖3 自上而下，對應于圖2的速度、壓力、磁場分布和有效磁場圖

原文鏈接：https://doi.org/10.1016/j.jcp.2025.114209

(核稿：秦毅 編輯：張景會)